

In the explicit formula "d(n-1)" means "the common difference times (n-1), where n is the integer ID of term's location in the sequence." In the iterative formula, "a(n-1)" means "the value of the (n-1)th term in the sequence", this is not "a times (n-1)." Even though they both find the same thing, they each work differently-they're NOT the same form. A + B(n-1) is the standard form because it gives us two useful pieces of information without needing to manipulate the formula (the starting term A, and the common difference B).Īn explicit formula isn't another name for an iterative formula. M + Bn and A + B(n-1) are both equivalent explicit formulas for arithmetic sequences. So the equation becomes y=1x^2+0x+1, or y=x^2+1ītw you can check (4,17) to make sure it's right Wang Lei and Amira were asked to find an explicit formula for the sequence 30. Converting recursive & explicit forms of geometric sequences. Substitute a and b into 2=a+b+c: 2=1+0+c, c=1 Converting recursive & explicit forms of geometric sequences. Then subtract the 2 equations just produced: Recursive equation for arithmetic sequence.

can be solved without an explicit formula. The explicit rule represents an arithmetic sequence with first term a 1 -6+8(1)2 and common difference d8. For example, many questions about convergence, monotony, fixed points etc.
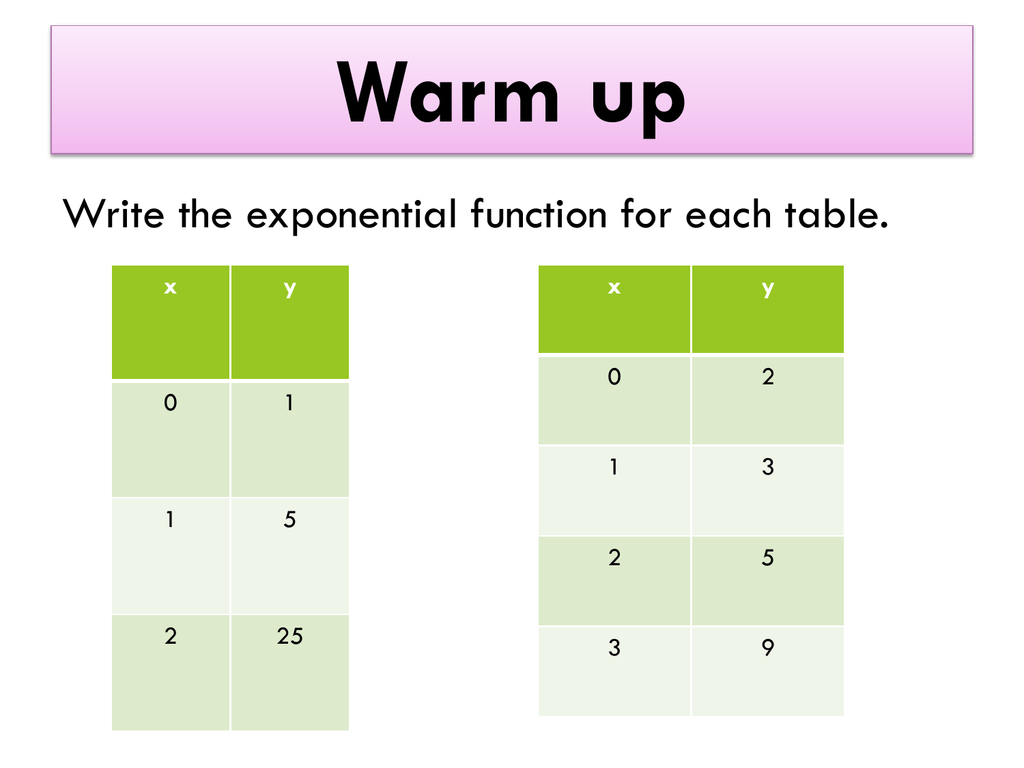
Solve this using any method, but i'll use elimination: Translating Between Recursive and Explicit Rules Example 6: Translating from Explicit Rules to Recursive Rules Write a recursive rule for (a) a n -6+8n and (b) a n -3½ (n-1). The function is y=ax^2+bx+c, so plug in each point to solve for a, b, and c. Let x=the position of the term in the sequence As an example, consider this recursive function definition, which defines the Collatz sequence: f(1) 0 f(2n) 1 + f(n) f(2n + 1) 1 + f(6n + 4) It's not known whether or not this is even a well-defined function or not.
Converting recursive sequence to explicit equation how to#
I know how to solve its characteristic equation and roots: 3 + 1, 3 - 1 0 This equation will give us one real solution and two imaginary solutions. In general, there is no algorithm for converting a recursive form into an iterative one. Since the sequence is quadratic, you only need 3 terms. I want to find the explicit formula for this difference equation. that means the sequence is quadratic/power of 2. However, you might notice that the differences of the differences between the numbers are equal (5-3=2, 7-5=2). This isn't an arithmetic ("linear") sequence because the differences between the numbers are different (5-2=3, 10-5=5, 17-10=7) Calculation for the n th n^\text=17 = 5 + 4 ⋅ 3 = 1 7 equals, start color #0d923f, 5, end color #0d923f, plus, 4, dot, start color #ed5fa6, 3, end color #ed5fa6, equals, 17


 0 kommentar(er)
0 kommentar(er)
